Aerodinámica Aerodynamics F1

Aerodinámica del Monoplaza

https://docs.google.com/spreadsheets/d/19bamJr_iKcQ5UR4ORA_S8aTfTQRMqx4b/edit?usp=drivesdk&ouid=102115123337297320834&rtpof=true&sd=true

F1 aerodinámica

f1-aerodynamic-grip-2

F1 aerodynamic grip 2 Radio 100

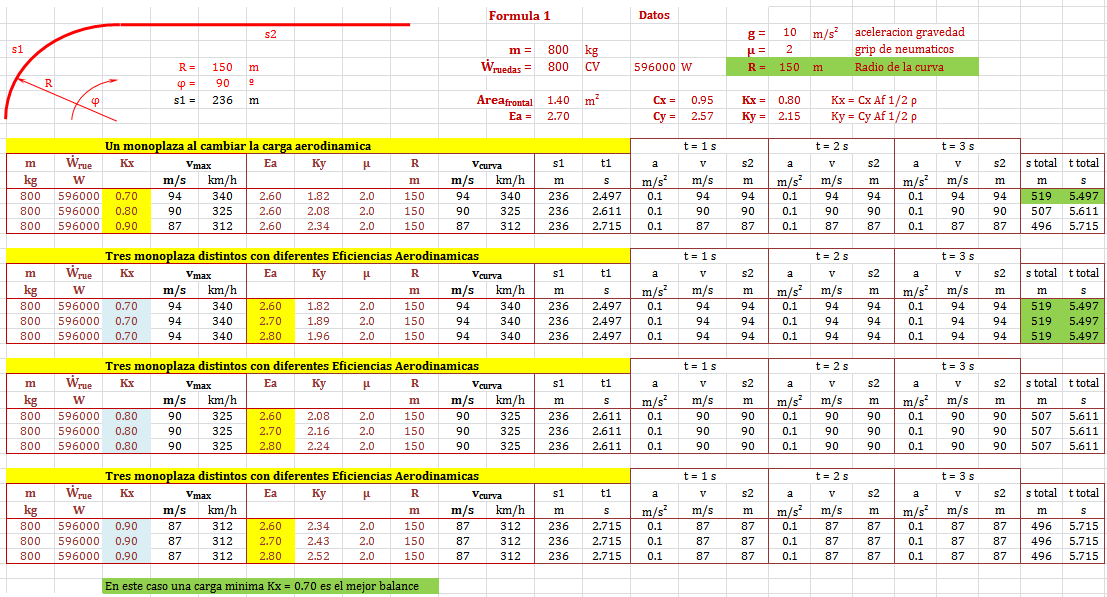
F1 aerodynamic grip 2 Radio 150

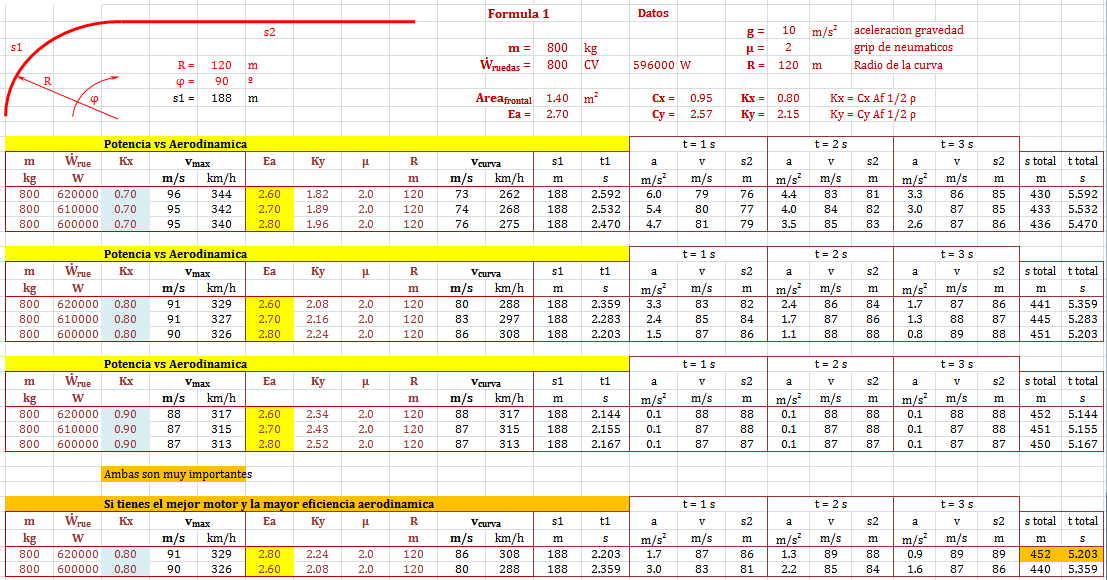
f1-potencia-vs-aerodynamic

F1 CFD Pressure Surfaces and Velocity Wheel

F1 CFD Temperature Surfaces

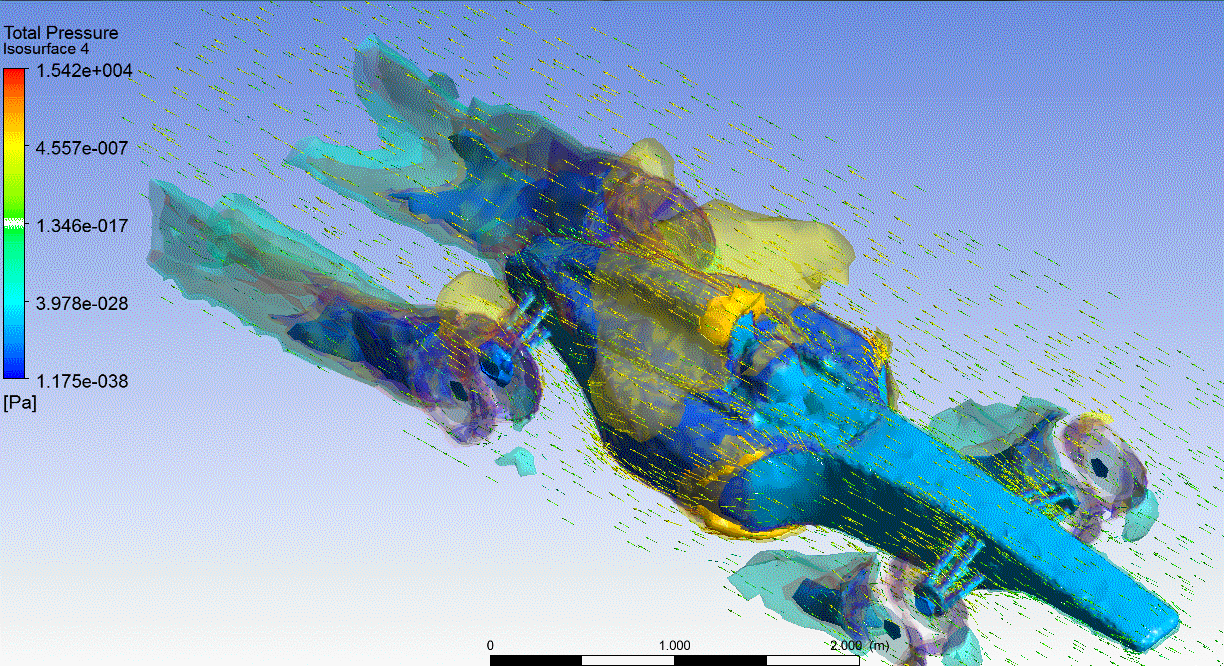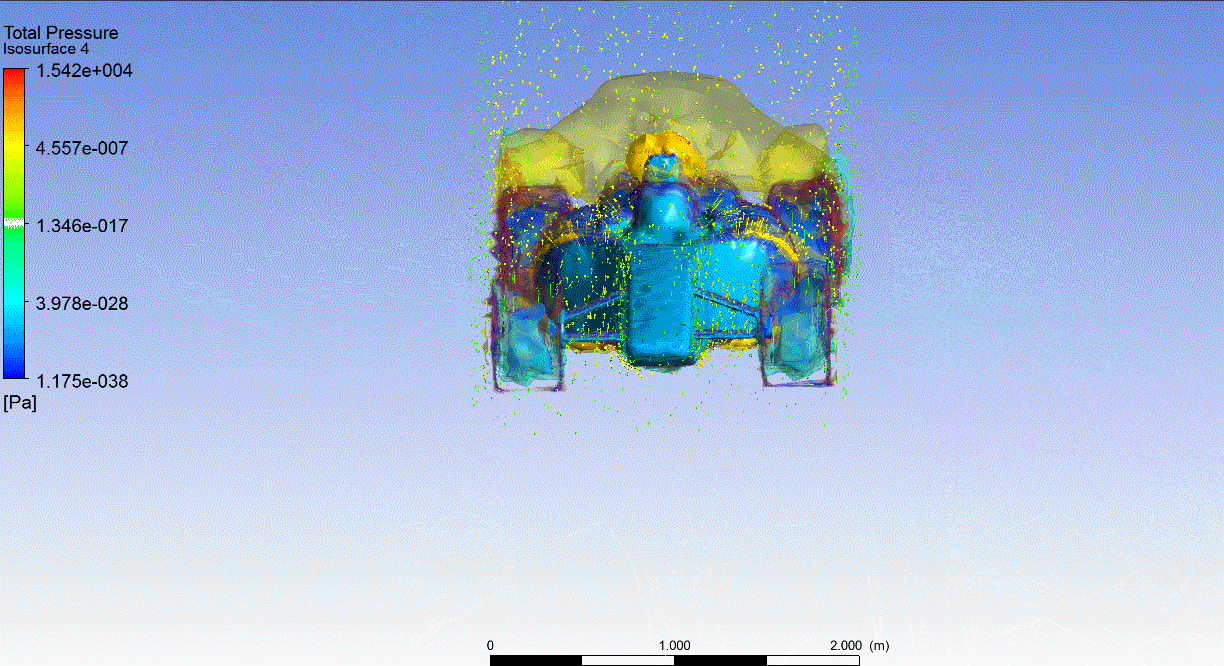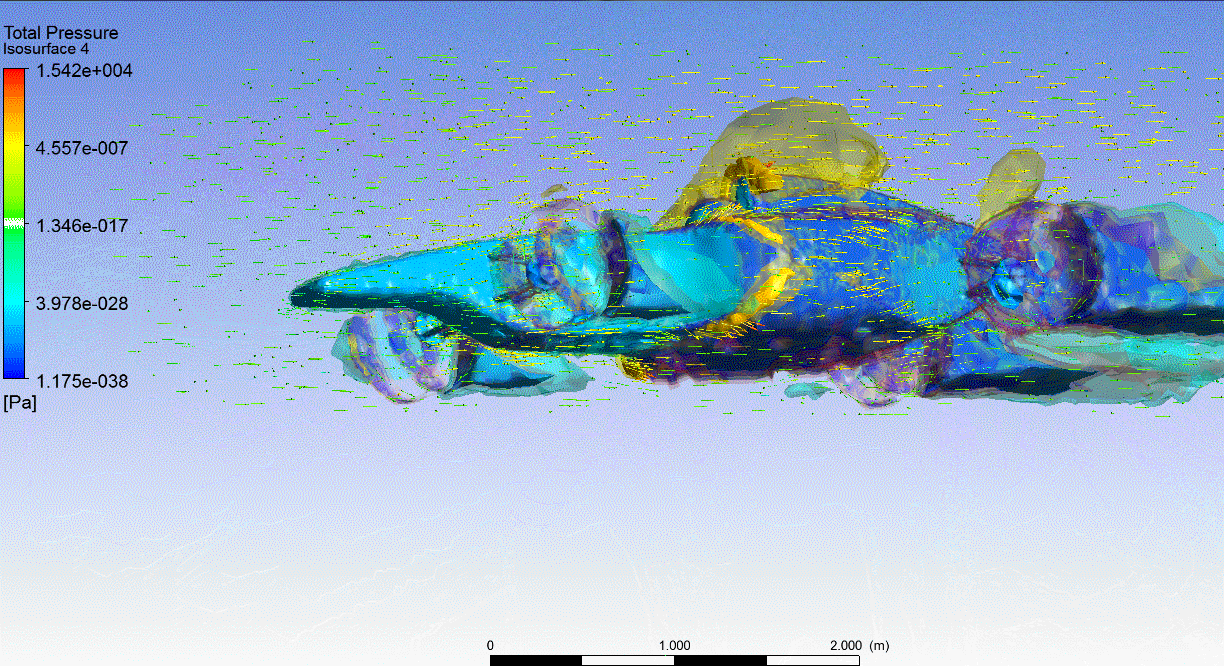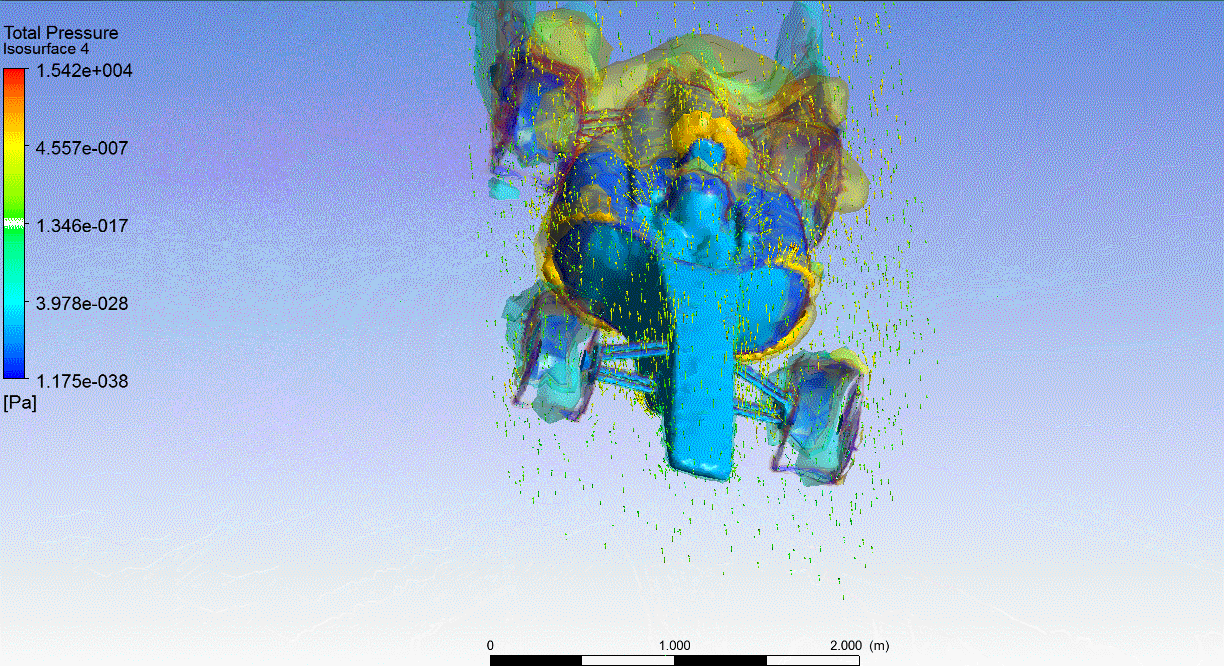
F1 CFD Pressure Isosurfaces Seudo Transparents and Velocities

F1 CFD Pressure Isosurfaces Seudo Transparents

F1-cfd-wheel-pressure-surfaces-and-velocity Aerodinámica de una Rueda

La aerodinámica es la rama de la mecánica de fluidos que estudia las fuerzas y centros de presiones que ejerce un fluido gaseoso, aire en este caso, sobre un cuerpo sólido.

Mediante fórmulas solo se pueden estudiar cuerpos sencillos (una esfera por ejemplo).

Para formas más complejas se emplean los elementos finitos, dividiendo la región de estudio en zonas con formas geométricas como cubos, tetraedros, etc.

Para resolver este sistema de mogollón de ecuaciones e incógnitas se utiliza el ordenador y un software CFD.

Para que un sólido de geometría sencilla, experimente la menor resistencia al avance, ésta debe tener una forma parecida a una lágrima.

La naturaleza nos muestra ejemplos de formas óptimas como el halcón peregrino haciendo un picado, delfines, etc.

A mayor velocidad esta forma se estiliza y se convierte en un alerón.

Mediante el Kutta–Joukowski theorem se diseñan formas óptimas de alerones (teóricamente).

A velocidades próximas a la del sonido, 340 m/s, o superiores el tema cambia (pero no es nuestro caso, un F1 alcanza ≈ 90 m/s = 324 km/hora).

Objetivos: valores de FD FL μ de los monoplazas F1

La velocidad máxima en recta depende de la Potencia del motor a máximas rpm Ẇmax y de la Drag Force FD.

La aceleración en frenada Gforce depende del Coeficiente de Rozamiento μ y de la Drag Force FD.

La velocidad del paso por curva depende, además del radio de la curva, del Coeficiente de Rozamiento μ y de la Lift Force

Potencia máxima del motor depende del régimen de giro (para n = 18.000 rpm)

Ẇ_max = 750 CV = 750 CV * 735 w/CV ≈ 550.000 w

Potencia máxima en las ruedas (para n = 18.000 rpm). Supongamos unas pérdidas por transmisión, bombas, rodadura, etc del 20%

Ẇ_{max ruedas} **≈ 550.000 w * 0,80** ≈ 440.000 w

jasf1961 F1 CFD Cálculo Objetivos

Con los valores Gforce sacados de la TV hemos calculado de forma aproximada los valores de

μ ≃ 1,18 FD ≃ 5.000 N FL ≃ 14.000 N EA ≃ FL/FD ≃ 2,8

Haciendo la simulación con la Dinámica vemos que los valores calculados se aproximan bastante en el caso de la frenada a máxima velocidad: N1 μ FL1 FD1

jasf1961 F1 CFD Cálculo Objetivos con Dinámica Frenando v máx DRS CERRADO

Y en el paso por curva son parecidos N2 μ FL2 FD2 y difiere el Radio de la Curva,

Rcur 185 m ≠ 222 m fundamentalmente porque las ruedas interiores apenas apoyan y deslizan:

jasf1961 F1 CFD Cálculo Objetivos con Dinámica En curva rápida a v2 cte

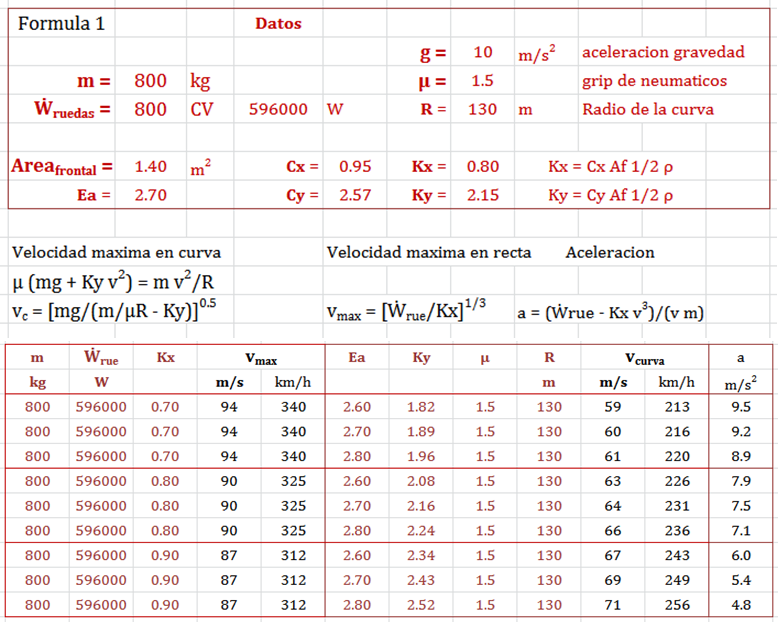
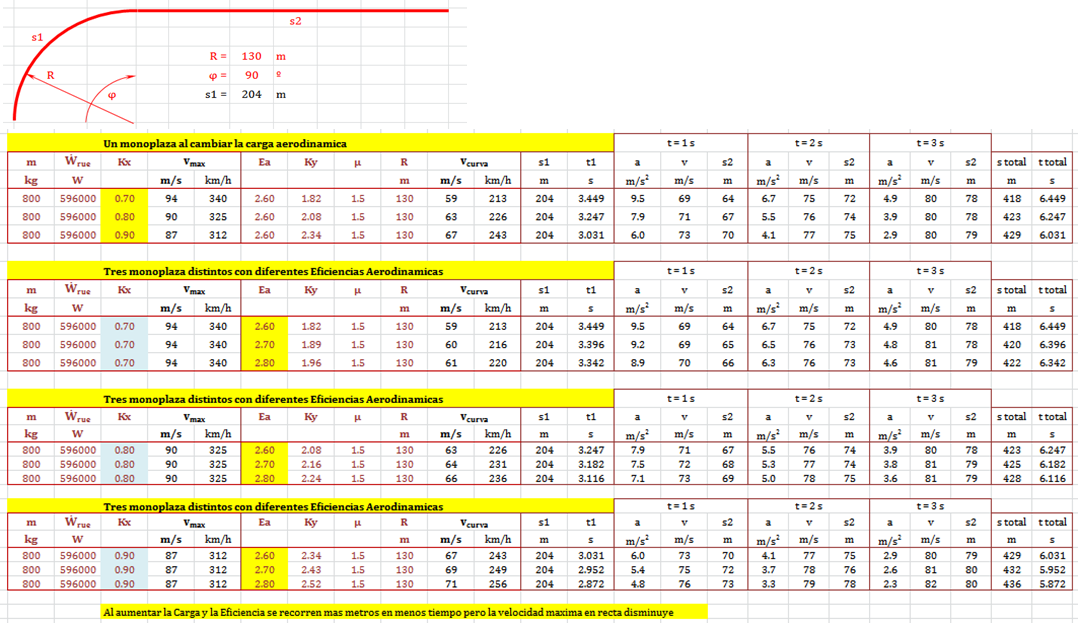
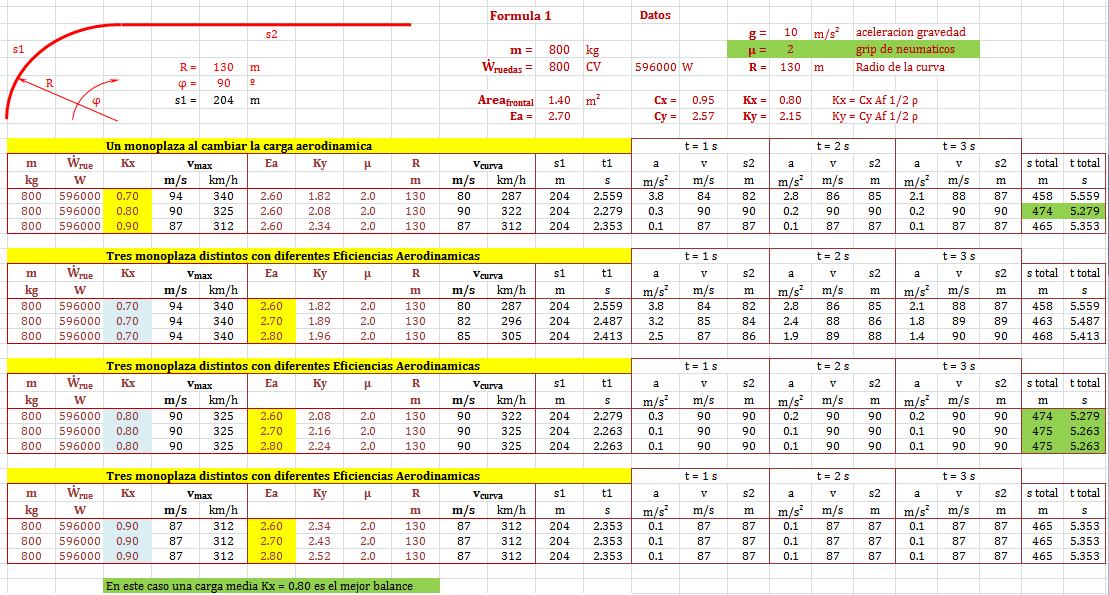
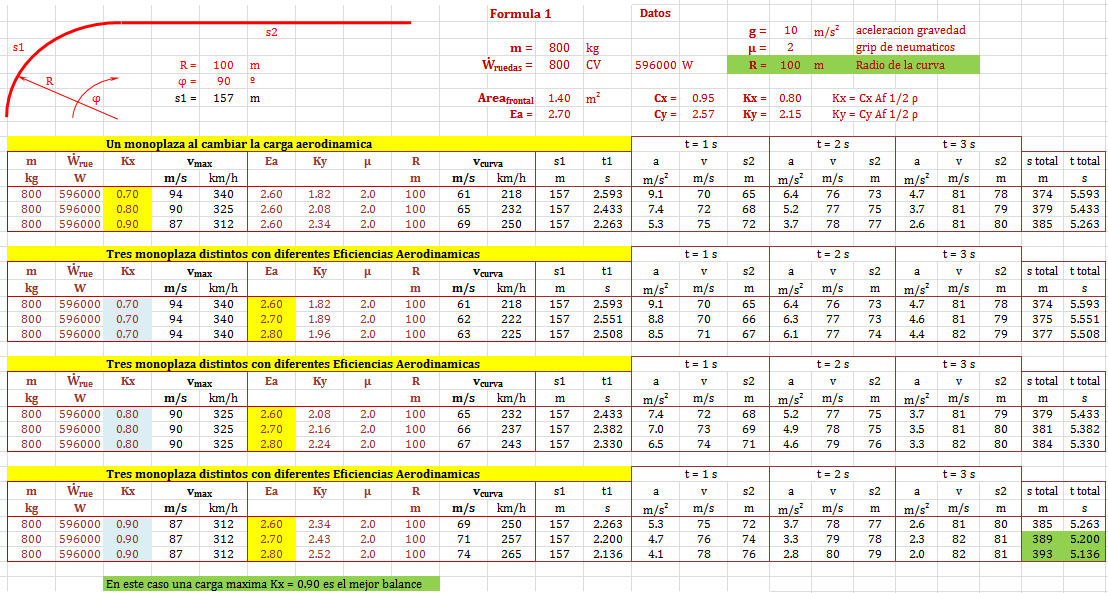
Velocidad máxima depende de la carga aerodinámica (en un circuito determinado)

v_max = 305 km/h = 300 km/h * 100 m/km * 3600 s/h ≈ 85 m/s

Con estos datos podemos calcular la Drag Force FD, ya que a la máxima velocidad toda la fuerza del motor se emplea en vencer dicha Drag Force (Fuerza de Arrastre), puesto que el monoplaza no es capaz de acelerar más:

FD = F_max ruedas = Ẇ_{max ruedas} / v_max = 440.000 w / (85 m/s) ≈ 5.100 N

La fuerza de sustentación Lift Force FL, condiciona el valor del Coeficiente de Rozamiento μ_roz.

Frenando, a la máxima velocidad, se alcanzan aceleraciones de 5G:

a = 5 g = 5 * 9,8 m/s^2 = 49 m/s^2

∑ F = m a

Eje X : FD + F_roz = m a Como F_roz = μ_rozN => FD + μ_rozN = m a => μ_rozN = m a – FD => N = (m a – FD) / μ_roz

Eje Y : N = FL + m g

Por tanto FL + m g = (m a – FD) / μ_roz=> FL = (m a – FD) / μ_roz– m g

Para m = 700 kg ( el coche sin gasolina + piloto son 640 kg) y μ_roz = 1,5 (150%)

FL = (m a – FD) / μ_roz– m g = (700 * 49 – 5.100)/ 1,5– 700 * 9,8FL = (34.300 – 5.100) / 1,5 – 6.860 ≈ 12.600 N

=> EA = 12.600 / 5.100 = 2,47

Para m = 800 kg y μ_roz = 1,0 (100%)

FL = (m a – FD) / μ_roz– m g = (800 * 49 – 5.100) / 1– 800 * 9,8 = FL = (39.200 – 5.100) / 1 – 7.840 ≈ 26.750 N

=> EA = 26.750 / 5.100 = 5,24

Para m = 750 kg y μ_roz = 1,2 (120%)

FL = (m a – FD) / μ_roz– m g = (750* 49 – 5.100) / 1,2– 750* 9,8 = FL = (36.750 – 5.100) / 1,2 – 7.350 ≈ 19.025 N

=> EA = 19.025 / 5.100 = 3,73

Para m = 750 kg y μ_roz = 1,5 (150%)

FL = (m a – FD) / μ_roz– m g = (750* 49 – 5.100) / 1,5– 750* 9,8 = FL = (36.750 – 5.100) / 1,5– 7.350 ≈ 13750 N

=> EA = 13.750 / 5.100 = 2,70

Por tanto, tomaremos como datos de partida:

Potencia del motor a las ruedas Ẇ_{max ruedas} ≈ 550.000 w * 0,80 ≈ 440.000 w

Drag Force FD ≈ 5.100 N para v_max ≈ 85 m/s (FD depende de la velocidad)

Lift Force FL ≈ 13.750 N (depende del μ_roz)para vmax ≈ 85 m/s (FL depende de la velocidad)

Eficiencia Aerodinámica EA = FL / FD ≈ 13.750 / 5.100 ≈ 2,70 (teóricamente es independiente de la velocidad)

Valores de FD y FL que deberíamos obtener en el CFD para que el monoplaza sea digno.

jasf1961 F1 CFD Datos Generales Simulación

jasf1961 F1 CFD Resultados Simulación Mod 1

Mod 1 EA ≃ 1,50

jasf1961 F1 CFD Resultados Simulación Mod 2

Mod 2 EA ≃ 0,80 En ambos casos Mod1 y Mod2 EA es menor de lo que debería ser.

Aerodynamics

En nuestro caso el fluido es el aire. Nos referiremos siempre al aire, aunque lo dicho sea extensible a los fluidos en general.

Las fuerzas aerodinámicas en un sólido en general y en un perfil alar (alerón), en particular, son:

FD = CD Pd A siendo

FD, fuerza Drag de arrastre

Pd, presión dinámica

CD, coeficiente Drag de arrastre

A, Area

FL = CL Pd A siendo

FL, fuerza Lift de sustentación

CL, coeficiente Lift de sustentación

Pd = ½ ( ρ v²) siendo

ρ, densidad del aire v, velocidad relativa entre el aire y el sólido

FD = CD Pd A = CD ½ ( ρ v²) A

FL = CL Pd A = CL ½ ( ρ v²) A

CD = f (forma, ángulo de ataque, espesor/cuerda, Nº Reynolds)

CL = f (forma, ángulo de ataque, espesor/cuerda, Nº Reynolds)

CD y CL dependen (son función) de la forma del sólido, del ángulo de ataque α, de v (velocidad relativa entre el aire y el sólido), de t / c espesor/cuerda del sólido, del Nº Reynolds, de la rugosidad del sólido,…

La relación EA = CL / CD = FL / FD = Lift / Drag = Sustentación / Arrastre se llama Eficiencia Aerodinámica. Cuanto mayor sea mejor.

Re = ρ v c / μ siendo Re, Nº Reynolds ρ, densidad del aire v, velocidad relativa entre el aire y el sólido

c, cuerda t, espesor μ, viscosidad dinámica del aire

Dado que la mayoría de estos parámetros, ρ v μ no los podemos cambiar, básicamente, solo podemos jugar con:

el ángulo de ataque α

y la forma del monoplaza o del alerón.

Aquí tenemos dos gráficas analizando CD = f (α) CL = f (α) EA = FL / FD = f (α) y dos alerones

Para sacar dichas gráficas se recurre a la simulación mediante Computer Fluids Dynamics, CFD o túneles de viento.

Eficicencia Aerodinamica EA CL CD

Bernouille

Imagen con presiones y velocidades.

Los colores del coche representan las presiones en Pa (azul baja, verde intermedia y rojo alta)

y las flechas las velocidades en m/s (azul baja, verde intermedia y rojo alta).

Plano de Corte ( Cut PLane) donde representamos las velocidades.

F1 Mix PLane Velocity

Con un software CAD hacemos el diseño 3D, y lo llevamos a un software CFD, realizamos el mallado con la máxima precisión posible que nos permita el ordenador (en un tiempo razonable) y hacemos la simulación aerodinámica – termodinámica (podemos incluir energías caloríficas de los escapes, pontones, neumáticos…).

Los cálculos se hacen para una velocidad (75 m/s ó 90 m/s por ejemplo) y con el análisis dimensional se calculan para el resto de velocidades (en teoría CD y CL no deberían variar), aunque vemos que según el CFD hay ligeros cambios en CD y CL pero apenas cambia el valor de la Eficiencia Aerodinámica, Ea).

Calculamos la Potencia, Ẇ, y otras variables (ver Motor).

Con un software CFD, Computer Fluids Dynamics, calculamos las fuerzas aerodinámicas y el lugar donde actúan, el Centro de Presiones:

FD Drag Force (Fuerza de Arrastre, opuesta al avance del monoplaza),

FL Lift Force (Fuerza de Sustentación), en nuestro caso invertida, que es la fuerza que empuja al coche hacia abajo y es conocida como Down Force

y el Centro de Presiones, Cp.

También tenemos otras fuerzas:

Fmot Fuerza del motor

mg Peso del mismo sentido que Lift Force, pero actuando en el Cm, el centro de masas (de gravedad) del F1

Froz Fuerza de rozamiento entre ruedas y asfalto. En aceleración y freno motor sólo tenemos en cuenta las ruedas traseras

Fi Fuerza de inercia Fi = ma

Fcent Fuerza centrífuga en las curvas, actuando en el Cm

En el CFD, para aerodinámica el método K – W SST suele dar los mejores resultados, aunque hay veces que para empezar el cálculo da Divergencias ( no es capaz de reducir los errores ) y hay que usar S – A para ver » por dónde van los tiros » y con los resultados obtenidos proseguir con K – W SST , o bien inicializar K – W SST pero en las Condiciones de Contorno y/o Limites podemos poner datos de los resultados obtenidos en S -A: ( por ejemplo limitar Temperaturas T en ºK y/o Presiones en PA( Estáticas o Absolutas).

With a CAD software do 3D design, and took him to a CFD software, perform the meshing with the highest possible accuracy that allows us to the computer (in a reasonable time) and do the simulation aerodynamics – thermodynamics (heat energy can include the escapes, pontoons, tires …).
Calculations are made for a speed (75 m / s or 90 m / s for example) and the dimensional analysis calculated for the remaining speeds (theoretical CD and CL should not vary), while according to the CFD see that there slight changes in CD and CL but just change the value of the Efficiency Aerodynamics Ea).

We calculate the power, W, and other variables (see engine).

With a CFD software, Computer Fluids Dynamics calculate the aerodynamic forces and the place where they work, the Center Pressures:

FD, Drag Force (Drag, opposed to the advancement of the car)

FL, Lift Force (Sustainability), in our case inverted, that is the force that pushes the car down and is known as Down Force

and the Center of Pressure, Cp.

We also have other forces:

Fmot, Motor Force

mg, Weight Lift Force same direction, but acting in the Cm, the center of mass (gravity) of F1

Froz, Force of friction between wheel and road. In acceleration, traction, we consider only the rear wheels

Fcent, cornering centrifugal force acting on the Cm

the weight mg, the same direction as the downforce, but acting in the Center of Mass, Cm,

Centrifugal Force on curves, Fc, which also operates in the Center of Mass, Cm

and the friction force between the tires and the asphalt, Froz, acting on the contact area of each wheel with asphalt.

In the CFD aerodynamic method for K – W SST usually gives the best results, but there are times to start the calculation gives Divergences (not able to reduce errors) and have to use S – A to see «where to go shots «and proceed with the results obtained with K – W SST, or initialize K – W SST but in Boundary Conditions and / or data limits can put the results in S-A: (eg limiting temperatures T in ° K and / or PA pressures (static or Absolute).